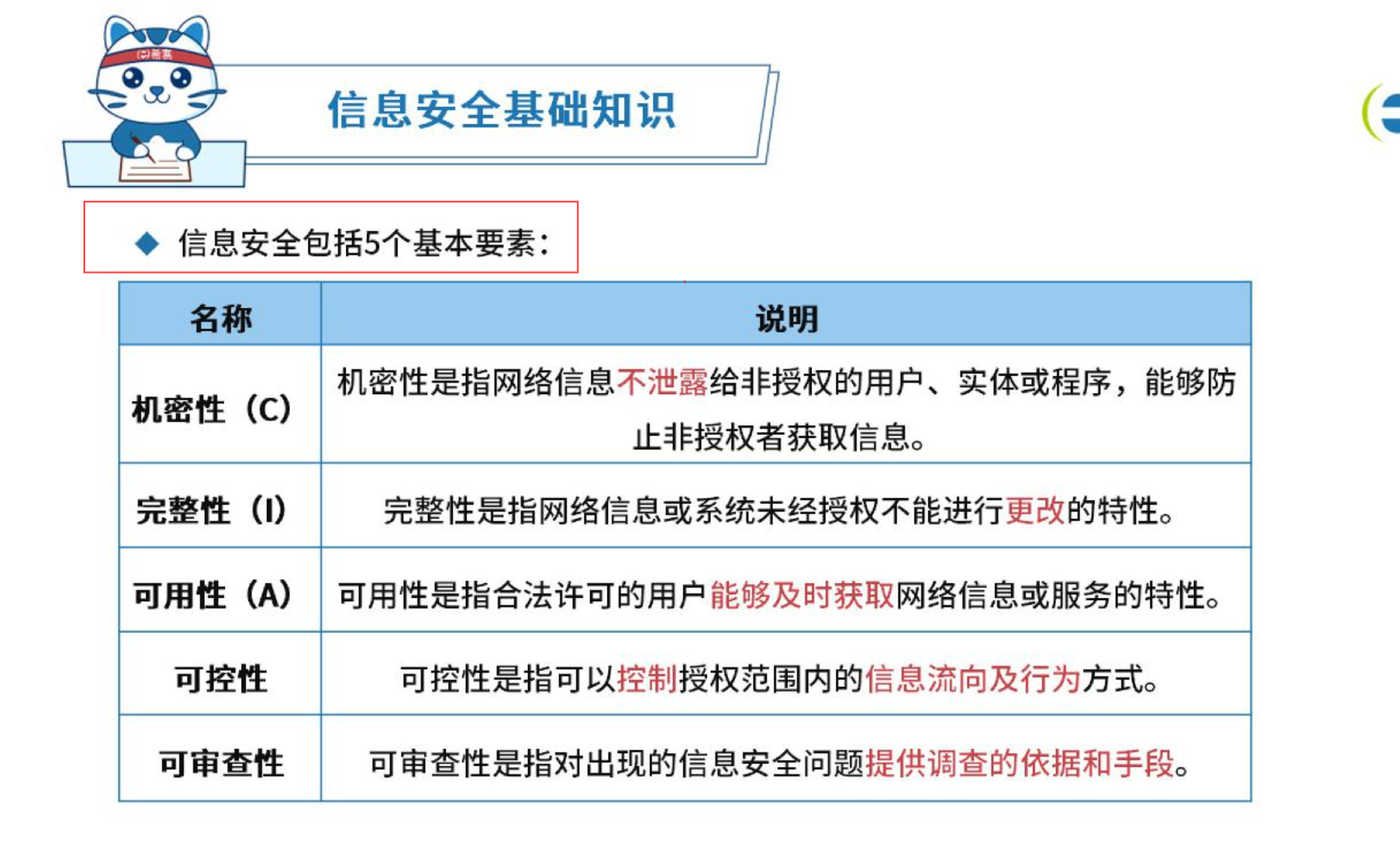
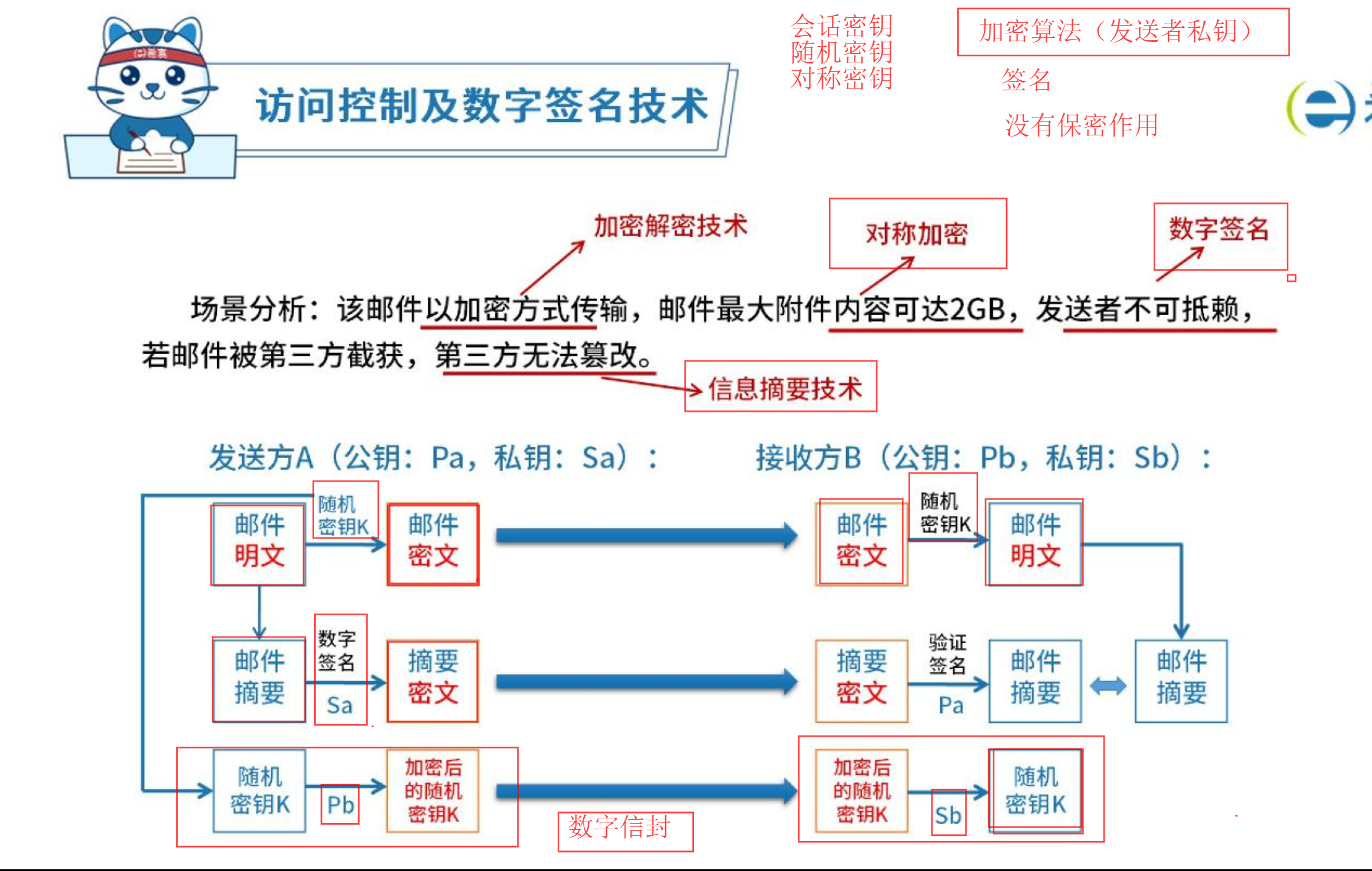
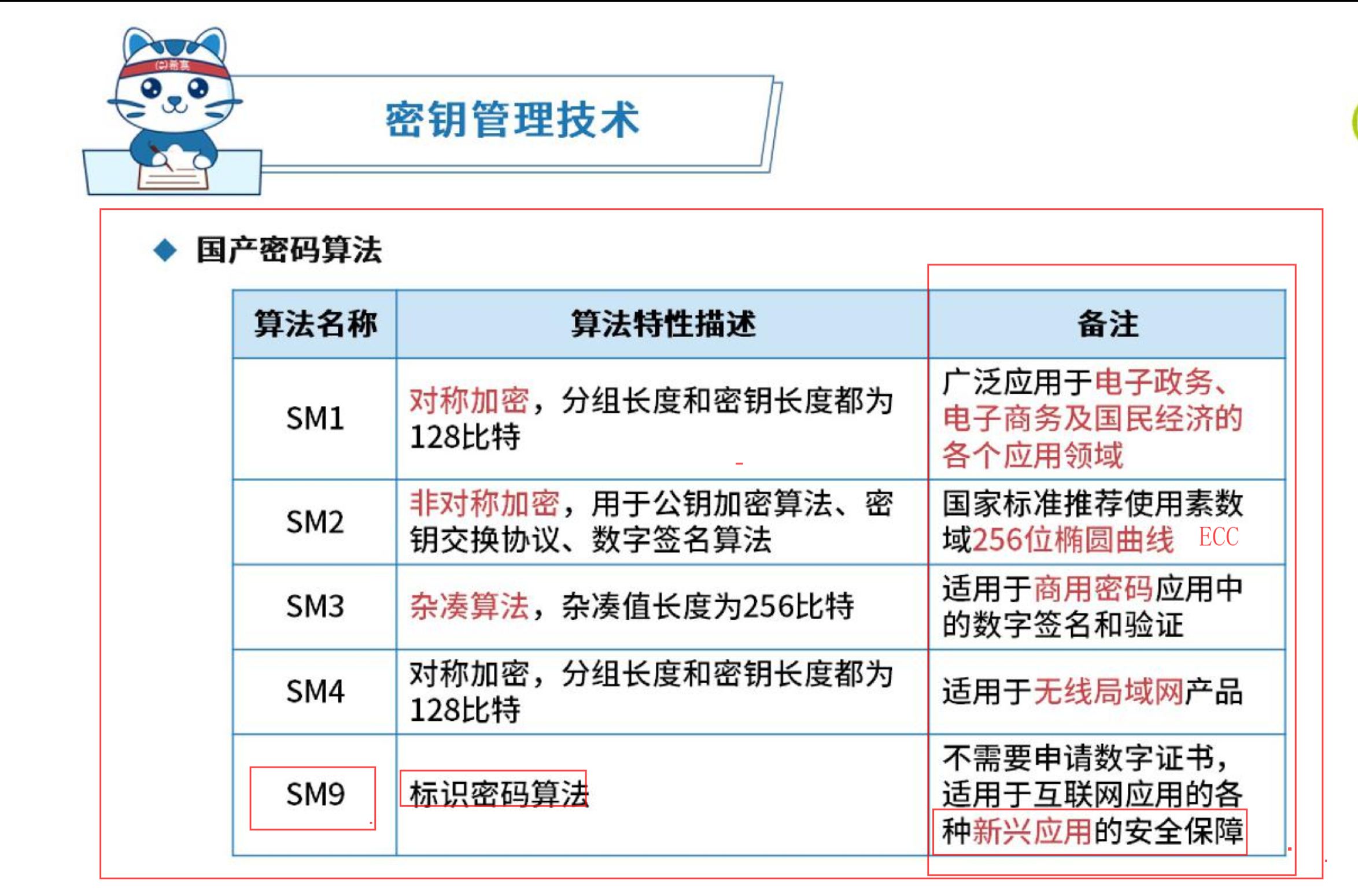
特么，差点照片全没了。。卧槽！！！！吓死我了！！！！感谢one driver。换nextcloud了

题目

论云原生架构及其应用
近年来，随着数字化转型不断深入，科技创新与业务发展不断融合，各行各业正在从大工业时代的固化范式进化成面向创新型组织与灵活型业务的崭新模式。在这一背景下，以容器和微服务架构为代表的云原生技术作为云计算服务的新模式，已经逐渐成为企业持续发展的主流选择。云原生架构是基于云原生技术的一组架构原则和设计模式的集合，旨在将云应用中的非业务代码部分进行最大化剥离，从而让云设施接管应用中原有的大量非功能特性(如弹性、韧性、安全、可观测性、灰度等)，使业务不再有非功能性业务中断困扰的同时，具备轻量、敏捷、高度自动化的特点。云原生架构有利于各组织在公有云、私有云和混合云等新型动态环境中，构建和运行可弹性扩展的应用，其代表技术包括容器、服务网格、微服务、不可变基础设施和声明式API等。请围绕“论云原生架构及其应用”论题，依次从以下三个方面进行论述:
1.概要叙述你参与管理和开发的软件项目以及承担的主要工作。
2.服务化、弹性、可观测性和自动化是云原生架构的四类设计原则，请简要对这四类设计原则的内涵进行阐述。
3.具体阐述你参与管理和开发的项目是如何采用云原生架构的，并且围绕上述四类设计原则，详细论述在项目设计与实现过程中遇到了哪些实际问题，是如何解决的。

简介

近些年，新能源汽车蓬勃发展，我司开发了一个针对新能源汽车的一体化平台，该平台主要包括新闻、社区、车型库等主要模块。我在该项目中担任技术经理，负责系统方案定制与技术指导工作。本文描述了该项目中云原生架构的实施过程与解决方案，主要分三个部分，?

背景

2022 年，新能源汽车蓬勃发展，国家也出台了相应政策法规予以支持，但市面上并没有针对新能源汽车的平台，用户在搜索新能源车型的时候，无法快速准确的找到相关信息。为响应国家号召，满足用户需求，于是我司决定开发一个针对新能源汽车的一体化平台。
该项目于 2022 年 6 月开始，团队成员共 17 人，我在该项目中担任技术经理，主要负责系统方案定制与技术指导工作。项目主要有三个主要模块：新闻、社区、车型库。其中新闻模块是为用户提供最新的新能源汽车消息，主要功能有：图文、视频、简讯、最新车型等。社区模块为用户提供一个讨论新能源车型的渠道，主要功能有：话题、帖子、车友圈、车型打分等。其中车型库是该项目的核心，我们在传统汽车平台的基础上增加了许多新能源汽车特有功能，比如辅助驾驶、智能座舱、三电系统等，并对这些功能做了相应评测，建立了对应的评测系统。以此为基础，建立了车型榜单、选车等功能。

回应

云原生架构由于其轻量、敏捷、高度自动化且成本相比传统方式更低等特点，已是目前企业发展的主流选择。云原生架构的设计原则有服务化、弹性、可观测性、自动化，其中服务化原则，是将整体业务拆分为大小适中的服务，解决大型项目中单体架构，开发难，部署难等问题。弹性原则，充分利用云服务的计算资源，动态伸缩，满足用户高峰时段的访问需求，降低低谷时段的成本，做到即用即申请，解决传统方式中扩容难，成本高等问题。可观测性原则，因为服务微型化，用户的请求会经过多个服务，当出现问题的时候，定位排查较为困难，需要提高其可观测行，一般使用链路追踪技术解决。自动化原则，当服务不断增长，人工部署成本较高，此时需引入自动化运维等相关技术，降低运维成本，提高运维效率。

过度

一个良好的云原生架构应是结构清晰、扩展方便、高度自动化的，以下就该系统的设计、开发、运行三个阶段论述该项目的实施过程与解决方案。
// serverless
// devops
// 微服务
// 服务端架构
//

正文

整体架构

该项目是一个针对 C 端用户的一体化平台，考虑到应用推广、开发成本等因素，应用部分采用 B/S 架构。传统 B/S 架构一般为单体架构，用 MVC 模式进行开发，这种架构在复杂应用上的缺点较多，开发人员需要在一个代码仓库内进行修改，且每次更新都需要重新启动，牵一发而动全身，项目的维护成本较高。所以我们采用前后端分离的 B/S 架构，前端部分使用基于 React 的全栈框架 NextJS，方便 SEO，满足推广需求，业务人员可以专注于自己擅长的领域，提高开发效率。后端业务部分为微服务架构，将应用拆解为不同的服务，使用公司提供的 DevOps 工具平台，自动化独立部署项目，方便业务拆解分配到各个项目组，提高开发运维效率，满足自动化要求。数据库部分，独立于业务系统，主要分两个部分，缓存部分使用 Redis 数据库，提高系统的并发吞吐。业务数据使用 Mysql 数据库，保证数据的原子性、一致性、持久性、隔离性。用户请求到达防火墙后，进入 VPC 内网，依次通过负载均衡、API 网关、微服务集群、数据库集群，返回响应内容。该方案整体结构清晰、高度自动化，服务拆分明确，满足云原生架构的自动化、服务化原则。

服务端

后端服务采用业务拆分的方式，主要包括：新闻、社区、车型库、用户、搜索等服务。服务之间采用 http 协议在 VPC 内网中通信，使用 REST 风格，该风格以资源为中心，请求方式作为对资源的操作，GET 表示对资源的获取，POST 表示对资源的新增，PUT 表示对资源的全量更新，PATCH 表示对资源的部分更新，DELETE 表示删除资源，可以有效的降低沟通成本。每个微服务部署在 ServerLess 上，

DevOps

结论

该项目于 2023 年 10 月上线，稳定运行至今，未出现重大事故。由于项目扩展性良好，于二期工程增加了移动设备适配，服务端少量修改后顺利上线安卓与 IOS 平台。项目运行过程中也遇到了一些问题，比如 Serverless 冷启动问题，当已有实例无法满足用户访问需求的时候，需要动态扩容，增加实例。这时云厂商会创建 VPC，拉取镜像，成功启动后才能响应用户请求，整个过程耗时数秒，用户体验较差。由于大部分环节由云厂商控制，我们无法直接参与，所以采取的方案主要有两个，一个是将镜像服务放在同一个可用区，从内网进行拉取，并精简镜像体积，提高镜像拉取速度。二是在用户访问高峰时段，预留一部分启动实例，减少冷启动次数。目前冷启动概率已明显降低，镜像裁剪还有优化空间。

题目

1、预计:项目信息
2、软件维护的主要内容，提高可维护性的常见方法
3、预计:结合项目说明具体实施过程/遇到的问题及解决方案

简介

近些年，新能源汽车蓬勃发展，我司开发了一个针对新能源汽车的平台，主要包括了：媒体、社区、车型库等模块。我在该项目中担任技术经理，负责系统方案设计及技术指导工作。本文描述了该项目中维护性方面的设计与实施过程，主要包括应用端、服务端、部署运行三个部分。应用端采用 Nodejs 同构框架 NestJS，使用 Typescript 进行代码编写，提高了可阅读性、可修改性。服务端采用分层设计，并使用 REST 风格与应用端通信，并生成标准的 OpenAPI 文档，有效提高了可修改性、可阅读性。部署与运行阶段，采用 CI/CD 工具，实现了代码测试、打包、部署等功能，并使用 Serverless，提高了项目的可靠性、可移植性。

背景

2022 年，新能源汽车蓬勃发展，国家出台了相应的政策支持，此时市面上还没有专门针对新能源汽车的应用平台，用户在检索新能源车型信息的时候，无法快速准确的找到对应信息。为响应国家号召，满足用户需求，我司开发一个针对新能源汽车的一体化平台。

该项目于 2022 年 6 月开始，团队成员共 17 人，我在该项目中担任技术经理，主要负责系统方案定制及技术指导工作。该项目主要包括媒体、社区、车型库等主要模块，其中媒体模块主要为用户提供最新的新能源汽车新闻，主要功能有：简讯、文章、视频、最新车型等功能。社区模块为用户提供了讨论新能源车型的渠道，主要包括了：车友圈、热点话题、发帖、车型口碑等功能。车型库模块是该系统的核心，我们吸收传统汽车平台的经验，并在此基础上增加了一些新能源汽车特有的功能，比如三电系统、智能座舱、辅助驾驶等，并针对这些功能进行评测，建立了对应的评测系统。并由此延伸出选车、评测榜单等功能模块。

问题回应

软件的生命周期中，软件维护是提高系统寿命的一个主要手段，主要分四种维护类型，第一种是正确性维护，主要是修复系统中的 bug；适应性维护，系统状态或者系统数据变更后，系统需要进行更新或者迁移。完善性维护，当系统增加新功能或进行性能方面的优化属于该方面维护。预防性维护，适应未来的一种维护，比如专用的功能改成通用的功能。提高可维护性的常见方法有，提高可阅读性，完善的文档与规范的代码属于此类；提高可修改性，低耦合、高内聚的架构设计可以有效的提高可修改性；提高可测试性，测试是软件开发过程中不可或缺的环节，良好的系统可以更容易的进行测试；提升可靠性，一个稳定的软件，可以有效的降低维护成本。提升可移植性，应用软件的部署环境可能会发生变化，当环境变化时，如果我们采用环境无关的技术，比如 java 的虚拟机或者容器技术，可以有效的降低移植成本。

过度

一个良好的软件，应该是更容易维护的，以下就该系统的应用端、服务端、部署运行三个方面进行论述该项目的具体实施过程与解决方案。

正文

应用端

该项目是针对 C 端的汽车一体化应用平台，考虑到推广的便利性与开发成本，决定使用 B/S 架构。传统 B/S 架构中，一般会使用服务端渲染，但是这种方式，html 与后端的代码是放在一起的，可阅读性较差。这个时候，如果有功能需要进行维护，那么需要前端人员与后端人员同时在一个地方修改，因为前后端分工不同，这种方式明显降低了可修改性。所以我们决定使用前后端分离的方式，前端负责界面与功能交互，后端负责提供数据，降低耦合，提高可修改性。纯前端的应用，需要在浏览器使用 AJAX 技术去动态的获取后端数据，同时使用 Javascript 去渲染页面，最终通过拼接字符串或者模板的方式去生成 html 。这种方式因为没有 IDE 支持，可阅读性差，且修改也容易引起错误，可修改性差，且 javascript 是一种脚本语言，没有类型系统，当项目复杂后，阅读与修改都比较困难。所以我们决定使用基于 React 的全栈同构框架 NextJS，并使用微软出品的语言 Typescript 进行代码编写，并编译成 Javascript 在浏览器与 Nodejs 环境运行。这种方式可以使用服务端渲染，满足推广要求。使用 NextJS 框架 react 技术栈，有 IDE 支持，对开发人员友好，可以方便的生成 html，同时又使用 Typesctipt 语言进行类型控制，极大提高了可阅读性与可修改性。

服务端

服务端采用分层架构，共 6 层，主要包括：中间件层、守卫层、管道层、路由层、服务层、数据层，使用层次化风格的架构，可以有效的降低耦合度，提高可修改性。在与前端的通信上，我们选择 REST 风格的架构，该风格以资源为中心，使用 HTTP 协议进行构建，用不同的请求方式表示对资源的操作，主要有 GET，表示对资源的获取，POST 表示对资源的创建，PUT 表示对资源的全量更新，PATCH 表示对资源的部分更新，DELETE 表示删除资源。这种方式降低了前后端开发人员的沟通成本，同时因为资源定义明确，可以有效的提高可阅读性。我们在使用 REST 风格的时候，也生成了接口文档，在路由层使用装饰器风格的注解，标注每个资源的路由、入参、出参等详细描述，并使用 OpenAPI 标准生成了对应的文档，使用 swagger 工具在开发环境展示，有效提高了可阅读性。同时因为有了对应的标准接口文档，我们可以使用自动化接口测试工具对其进行测试，提高了可测试性。

部署与运行

该项目在设计阶段采用的是云原生架构，我们搭建了 DevOps 相关工具，代码版本管理工具使用 Git，并制定了代码的提交、质量规范，提交前进行预检，预检通过后，提交到 Gitlab 远程仓库，同时对应的负责人进行 Code Review，审核通过后合并对应分支，提升代码质量、可阅读性。当代码提交到指定分支后，自动运行代码检测工具，包括代码格式检测、单元测试等，提高了代码的可阅读性，降低了维护成本。检测通过后，使用容器化技术，将应用打包为 Docker 镜像，并提交到镜像仓库，提高了可移植性。打完完毕后，我们使用云厂商的服务，将应用镜像部署在 Serverless 上，即用即付，有效降低了运行成本，同时使用资源冗余的方式，多实例运行，自动伸缩，提高了应用的可靠性。同时在数据库层面上，我们使用的一主多从的方式进行部署，当某台数据库宕机后，可以自动切换其他节点，提高了可靠性。

结语

该项目于 2023 年 10 月上线，整体运行良好，未出现重大事故。后续我们做了一些完善性的维护，比如在服务端的数据层增加了缓存模块，由于该项目可修改性、可测试性良好，少量改动后便顺利上线。二期工程增加了移动端应用，因为采用 REST 风格架构，文档完善，可阅读性较好，后续也顺利上线。在项目的运行过程中，也遇到了一些问题，比如 Serverless 的冷启动问题，假如服务第一次启动，那么需要云厂商构建 VPC 网络，同时要下载镜像，同时启动镜像成功后，服务才会返回对应的数据，该过程耗时多达数秒，用户体验较差。 因为 serverless 其中一部分功能由云厂商控制，部分环节我们无法参与，所以我们只能对其中一部分功能做优化，比如裁剪镜像体积，降低云厂商拉取镜像的时间。根据不同时段的流量进行预留启动实例，降低冷启动概率。目前冷启动时间与概率已有所降低，镜像裁剪还有优化空间。

软件需求需要重新学一遍

论架构服务

• B/S 架构
• 分层架构
• Restful 架构

云原生主题论点

系统安全架构设计

• 访问控制
• 内外网隔离
• 开发环境与生产环境隔离

em

刚在想东西的时候发现。。

脑子里面空空如也

从小到大。。

我好像没有什么特别喜欢的爱好？？？

就特么离谱。。

计算机系统安全等级

• 自主级保护
• 系统审计级保护
• 安全标记保护
• 结构化保护
• 访问验证保护(最高等级)

构建的组装方式

• 顺序组装
• 层次组装
• 叠加组装

生命周期质量属性

• 开发期
• 运行期

软件复用三个阶段

• 获取可复用的资产（没办法直接用，得先构造）
• 管理可复用的资产
• 使用可复用的资产

架构权衡分析方法（ATAM）四种质量属性

• 性能
• 安全
• 可修改
• 可用性（实用性）

特定领域软件体系结构基本活动

• 领域分析，获取模型
• 领域设计，获取DSSA
• 领域实现，开发和组织可重用信息

系统测试的一句是 软件需求规格说明书

MIPS（每秒百万次指令数）的计算路径

一个指令为5个周期，每个周期3微秒 ，那么一个指令为 15 微秒。1秒 = 一百万微秒。一秒钟可运行 1 * 10^6 / 15 = 66666.66 次。约等于 0.067 百万次

公理

• 自反率 Y∈X∈U 这，X->Y 成立
• 增广率，若Z∈U且X->Y，则 ZX->ZY
• 传递率, 若 X->Y,Y->Z,则 X->Z
• 合并规则，如果 X->Y,X->Z,则 X->YZ
• 伪传递规则，X->Y,WY->Z，则 XW->Z
• 分解规则,X->Y及Z∈Y，则X->Z

常用协议

smtp : 25
pop3： 110
imap：143
ftp: 传输20 控制21

CMMI 软件能力评价，自顶向下

• 顶层方针
• 过程文件
• 规程文件
• 模板类文件

系统建模方法与基本工具

• 结构化建模工具为数据流图
• 信息建模方法工具是实体连续图(ERD)
• 面向对象为UML

需求管理需要重新确认

中间件提供两种不同类型的支持

• 交互支持
• 提供公共服务

软件脆弱性

系统可靠性分析于设计

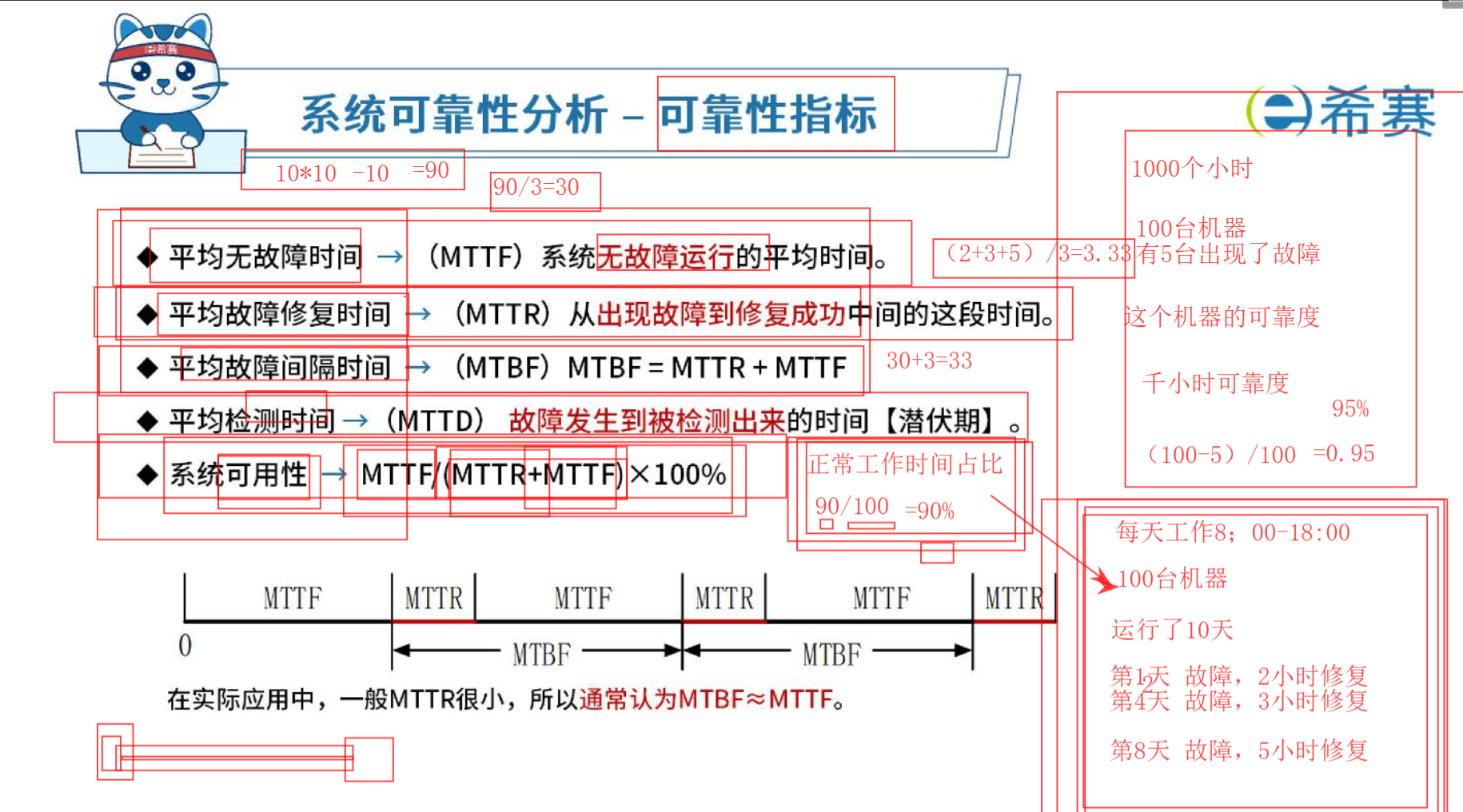
可用性= 可用时间 / 总时间

串并联模型

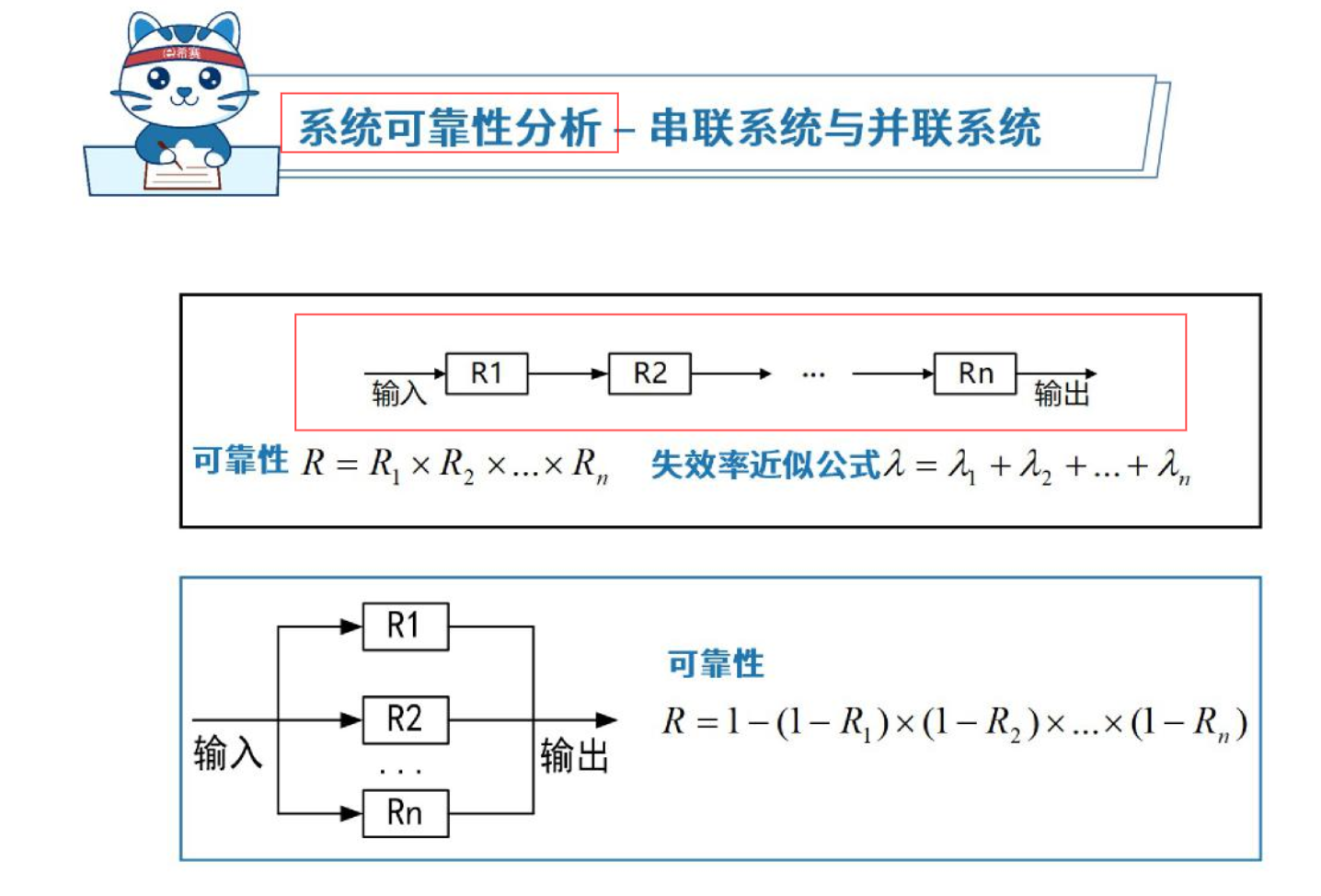
串联可靠性(任意是一个失效的概率) = r1 可靠性 * r2 可靠性 * rn 可靠性
并联可靠性（同时失效的概率）= 1 - 串联可靠性

可靠性设计

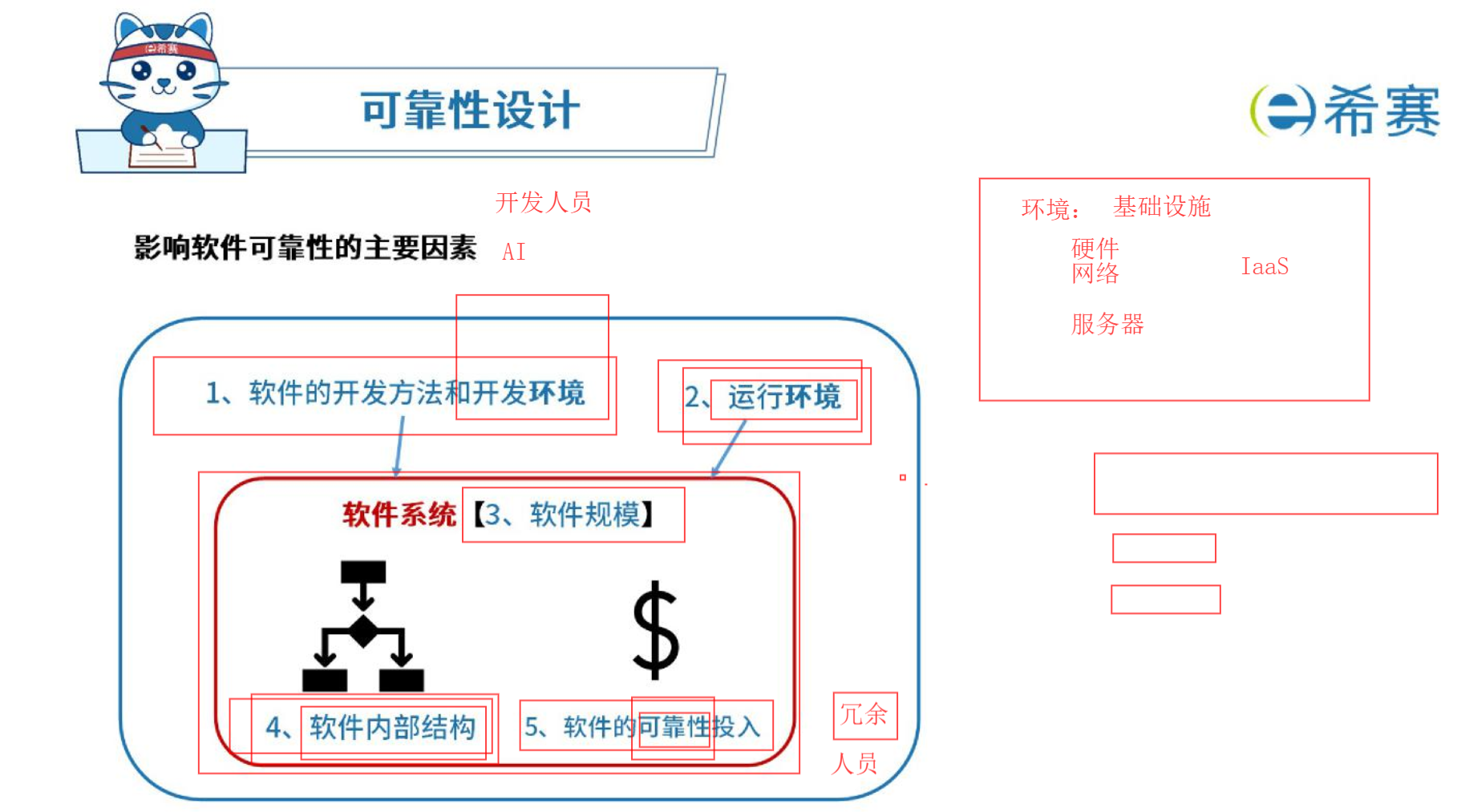
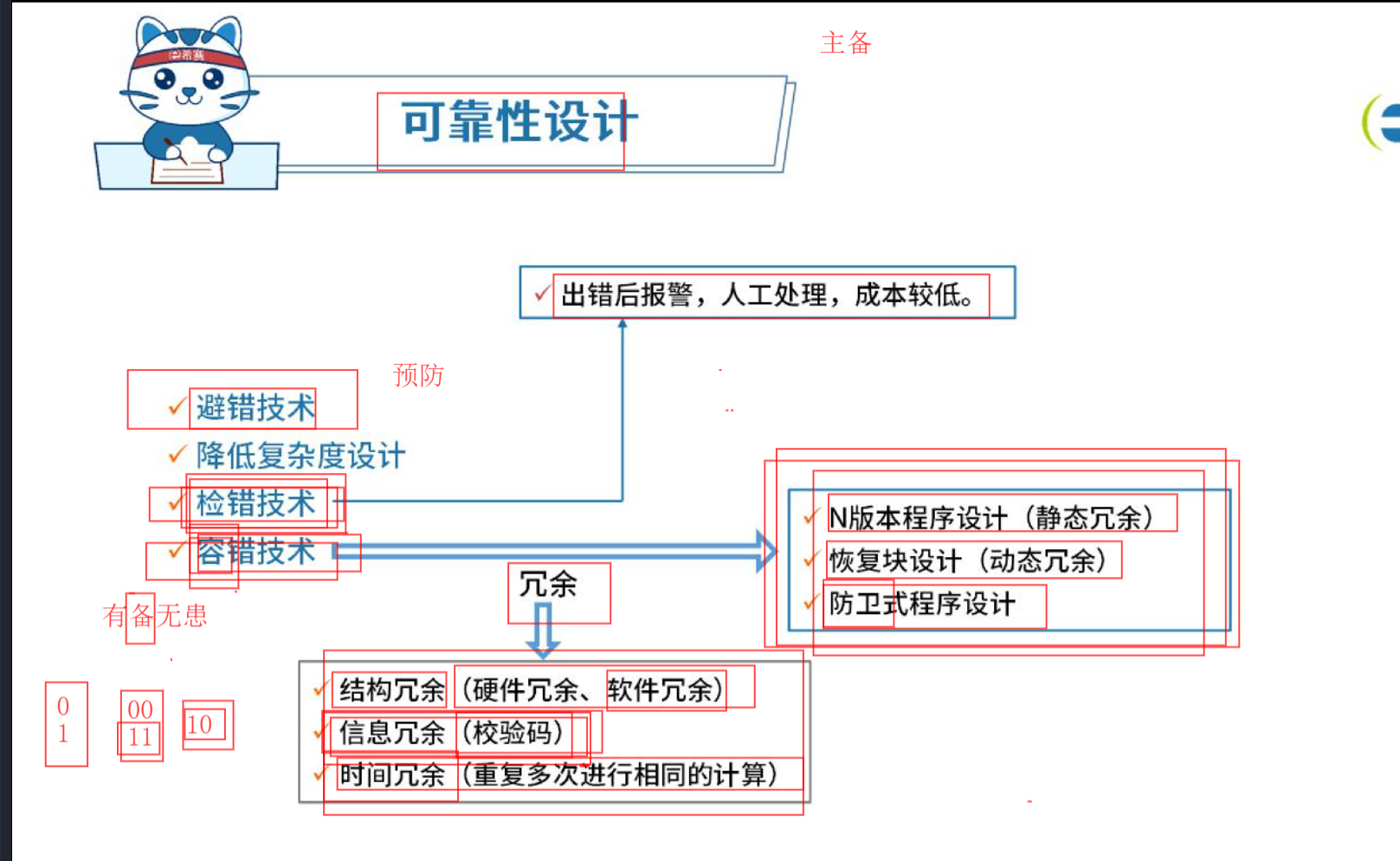
• N 版本冗余方案 (多个版本计算，交给表决器，表决出一个结果)，并联
• 恢复块方法（主块运行，验证不合格，交给后备块，直到最后一个后备块，直到通过验证通过，通过后执行，不合格异常），串联
• 防卫式程序设计（发现错误后，能撤销错误状态，恢复到一个已知的正确状态中去）
• 双机容错（一台出错，另外一台可用）
• • 双机热备（主系统出错后，备用系统才启用）
• • 双机互备（同时提供不同的服务，心跳出错，另外一台接管）
• • 双机双工（集群）

待复习

软件能力成熟度
设计模式
工作流参考模型
测试
UML
需求工程
ATAM
质量属性场景
ABSD
效用树
DSSA
关系代数

信息安全基础知识

五个基本要素

• 机密性
• 完整性
• 可用性
• 可控性
• 可审查性
  

信息安全范围

• 设备安全
• 内容安全
• 数据安全
• 行为安全

信息存储安全

数字签名

国密

云原生架构

• 服务化
• 弹性
• 可观测
• 韧性
• 自动化
• 零信任
• 架构持续演进